SET & FUNCTIONS

Set function

In mathematics, a set function is a function whose input is a set. The output is usually a number. Often the input is a set of real numbers, a set of points in Euclidean space, or a set of points in some measure space.

Examples

Examples of set functions include:

• The function that assigns to each set its cardinality, i.e. the number of members of the set, is a set function.
• The function

${\displaystyle d(A)=\lim _{n\to \infty }{\frac {|A\cap \{1,\dots ,n\}|}{n}},}$

Definition

A set is a well-defined collection of distinct objects. The objects that make up a set (also known as the elements or members of a set) can be anything: numbers, people, letters of the alphabet, other sets, and so on.

Membership

If B is a set and x is one of the objects of B, this is denoted x ∈ B, and is read as "x belongs to B", or "x is an element of B". If y is not a member of B then this is written as y ∉ B, and is read as "y does not belong to B".

For example, with respect to the sets A = {1,2,3,4}, B = {blue, white, red}, and F = {n² − 4 : n is an integer; and 0 ≤ n ≤ 19} defined above,

4 ∈ A and 12 ∈ F; but

9 ∉ F and green ∉ B.

Subsets

If every member of set A is also a member of set B, then A is said to be a subset of B, written A ⊆ B (also pronounced A is contained in B). Equivalently, we can write B⊇ A, read as B is a superset of A, B includes A, or B contains A. The relationship between sets established by ⊆ is called inclusion or containment.

If A is a subset of, but not equal to, B, then A is called a proper subset of B, written A ⊊ B (A is a proper subset of B) or B ⊋ A (B is a proper superset of A).

A is a subset of B

Example:

• The set of all men is a proper subset of the set of all people.
• {1, 3} ⊆ {1, 2, 3, 4}.
• {1, 2, 3, 4} ⊆ {1, 2, 3, 4}.

The empty set is a subset of every set and every set is a subset of itself:

• ∅ ⊆ A.
• A ⊆ A.

Every set is a subset of the universal set:

• A ⊆ U.

An obvious but useful identity, which can often be used to show that two seemingly different sets are equal:

• A = B if and only if A ⊆ B and B ⊆ A.

A partition of a set S is a set of nonempty subsets of S such that every element x in S is in exactly one of these subsets.

Power sets

The power set of a set S is the set of all subsets of S. The power set contains S itself and the empty set because these are both subsets of S. For example, the power set of the set {1, 2, 3} is {{1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3}, ∅}. The power set of a set S is usually written as P(S).

The power set of a finite set with n elements has 2ⁿ elements. For example, the set {1, 2, 3} contains three elements, and the power set shown above contains 2³ = 8 elements.

The power set of an infinite (either countable or uncountable) set is always uncountable. Moreover, the power set of a set is always strictly "bigger" than the original set in the sense that there is no way to pair every element of S with exactly one element of P(S). (There is never an onto map or surjection from S onto P(S).)

Basic operations

There are several fundamental operations for constructing new sets from given sets.

Unions

The union of A and B, denoted A ∪ B

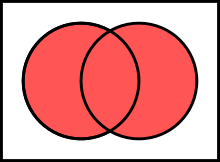
Two sets can be "added" together. The union of A and B, denoted by A ∪ B, is the set of all things that are members of either Aor B.

Examples:

• {1, 2} ∪ {1, 2} = {1, 2}.
• {1, 2} ∪ {2, 3} = {1, 2, 3}.
• {1, 2, 3} ∪ {3, 4, 5} = {1, 2, 3, 4, 5}

Some basic properties of unions:

• A ∪ B = B ∪ A.
• A ∪ (B ∪ C) = (A ∪ B) ∪ C.
• A ⊆ (A ∪ B).
• A ∪ A = A.
• A ∪ U = U.
• A ∪ ∅ = A.
• A ⊆ B if and only if A ∪ B = B.

Intersections

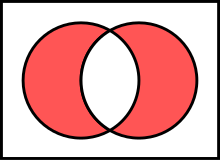
A new set can also be constructed by determining which members two sets have "in common". The intersection of A and B, denoted by A ∩ B, is the set of all things that are members of both A and B. If A ∩ B = ∅, then A and B are said to be disjoint.

The intersection of A and B, denoted A ∩ B.

Examples:

• {1, 2} ∩ {1, 2} = {1, 2}.
• {1, 2} ∩ {2, 3} = {2}.

Some basic properties of intersections:

• A ∩ B = B ∩ A.
• A ∩ (B ∩ C) = (A ∩ B) ∩ C.
• A ∩ B ⊆ A.
• A ∩ A = A.
• A ∩ U = A.
• A ∩ ∅ = ∅.
• A ⊆ B if and only if A ∩ B = A.

Complements

The relative complement
of B in A

The complement of A in U

The symmetric difference of Aand B

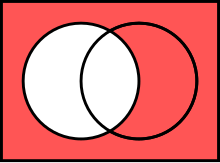
Two sets can also be "subtracted". The relative complement of B in A (also called the set-theoretic difference of A and B), denoted by A \ B (or A − B), is the set of all elements that are members of A but not members of B. Note that it is valid to "subtract" members of a set that are not in the set, such as removing the element green from the set {1, 2, 3}; doing so has no effect.

In certain settings all sets under discussion are considered to be subsets of a given universal set U. In such cases, U \ A is called the absolute complement or simply complement of A, and is denoted by A′.

• A′ = U \ A

Examples:

• {1, 2} \ {1, 2} = ∅.
• {1, 2, 3, 4} \ {1, 3} = {2, 4}.
• If U is the set of integers, E is the set of even integers, and O is the set of odd integers, then U \ E = E′ = O.

Some basic properties of complements:

• A \ B ≠ B \ A for A ≠ B.
• A ∪ A′ = U.
• A ∩ A′ = ∅.
• (A′)′ = A.
• ∅ \ A = ∅.
• A \ ∅ = A.
• A \ A = ∅.
• A \ U = ∅.
• A \ A′ = A and A′ \ A = A′.
• U′ = ∅ and ∅′ = U.
• A \ B = A ∩ B′.
• if A ⊆ B then A \ B = ∅.

An extension of the complement is the symmetric difference, defined for sets A, B as

${\displaystyle A\,\Delta \,B=(A\setminus B)\cup (B\setminus A).}$

For example, the symmetric difference of {7,8,9,10} and {9,10,11,12} is the set {7,8,11,12}. The power set of any set becomes a Boolean ring with symmetric difference as the addition of the ring (with the empty set as neutral element) and intersection as the multiplication of the ring.

Cartesian product

A new set can be constructed by associating every element of one set with every element of another set. The Cartesian product of two sets A and B, denoted by A × Bis the set of all ordered pairs (a, b) such that a is a member of A and b is a member of B.

Examples:

• {1, 2} × {red, white, green} = {(1, red), (1, white), (1, green), (2, red), (2, white), (2, green)}.
• {1, 2} × {1, 2} = {(1, 1), (1, 2), (2, 1), (2, 2)}.
• {a, b, c} × {d, e, f} = {(a, d), (a, e), (a, f), (b, d), (b, e), (b, f), (c, d), (c, e), (c, f)}.

Some basic properties of Cartesian products:

• A x B ≠ B x A for A ≠ B.
• A × ∅ = ∅.
• A × (B ∪ C) = (A × B) ∪ (A × C).
• (A ∪ B) × C = (A × C) ∪ (B × C).

Let A and B be finite sets; then the cardinality of the Cartesian product is the product of the cardinalities:

• | A × B | = | B × A | = | A | × | B |.